L’umorismo è una porta che si apre fulmineamente sull’intuizione dell’universale, una scorciatoia per ridurre le distanze ed approdare ad una percezione comune. Più prosaicamente, qualcuno (1) avrebbe anche dimostrato che esso può rappresentare una strategia didattica utile a rilassare il discente intimorito, contribuendo a ridurne l’ansia (da equazioni, per esempio) e ad indurlo psicologicamente ad affiancare, piuttosto che fronteggiare come fosse un nemico, il docente nel suo percorso esplicativo.

Vorrei presentare qui un piccolo elenco di aneddoti che, se non propriamente e spiccatamente umoristici, sono comunque in grado di suscitare una certa umana simpatia e che costellano la storia o, più in generale, il mondo, della fisica. Tenterò con questi aneddoti di perseguire un duplice obiettivo; da una parte cercherò di declinarne esplicitamente i rimandi epistemologici che è possibile individuare in essi: ciò che appare ad una prima lettura come qualcosa di buono per alleggerire i manuali o le conferenze, si rivelerà, ad una lettura più attenta, come utile strumento per allargare l’orizzonte a considerazioni tutt’altro che banali sullo status conoscitivo e metodologico della fisica. Una felice battuta o un aneddoto estemporaneo diventano così per la fisica l’equivalente di una formula ed aspirano a contenere un intero mondo di fenomeni nella ristrettezza di poche parole. Per quanto detto sopra, questi aneddoti rappresentano inoltre – è questo il mio secondo obiettivo – l’offerta di un’ulteriore possibilità didattica per gli insegnanti di fisica e di filosofia.

Ecco dunque immediatamente di cosa tratterò e con quale obiettivo: pinguini strumentalizzati, dinosauri immaginabili, guano fortunato, guardiani di vedetta e avidi ministri; ci sarebbero poi anche tacchini tronfi e draghi nel garage, ma su questi mi limiterò a pochi cenni, avendone già trattato altrove (2). I temi dell’epistemologia a cui questa sorta di improbabile “zoo” introduce sono quelli della visione strumentalistica o realistica della fisica, dell’imprevedibilità della scoperta, del sano e corretto ricorso alla quantificazione numerica e, infine, della controllabilità che caratterizza, comunque, le proposizioni scientifiche. A questo piano, si aggiungerà anche qualche considerazione di stampo più sociologico che strettamente epistemologico.

Iniziamo dunque a percorrere le strade dello “zoo” di cui sopra.

Il penguin diagram, diagramma a pinguino, è una rappresentazione utilizzata in fisica teorica per descrivere i processi di interazione tra alcune particelle elementari.

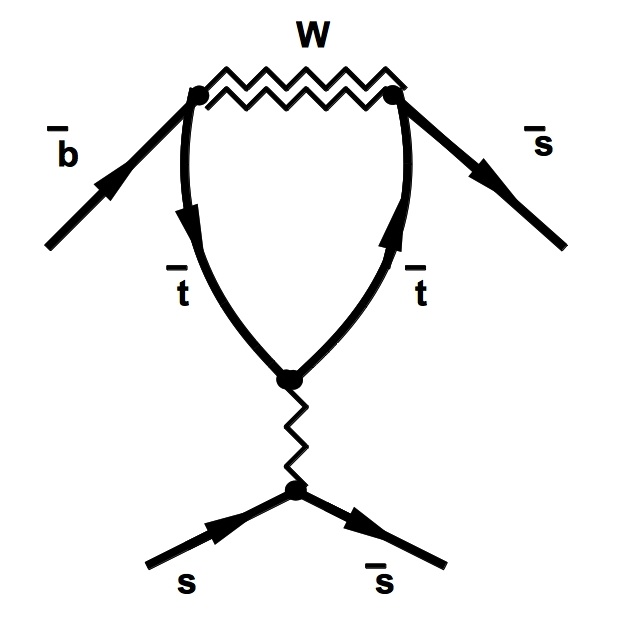
Diagramma a pinguino che rappresenta interazioni tra gli antiquark b,s,t e il quark s tramite lo scambio di un gluone (linea a zigzag verticale) e un bosone vettoriale intermedio W

Questo diagramma, detto a pinguino perché, con un po’ di fantasia, ricorda la figura di un pinguino, è un esempio della più generale famiglia dei cosiddetti diagrammi di Feynman. Richard Feynman (1918-1988), uno dei maggiori fisici del secolo scorso, elaborò questo metodo grafico come strategia pratica per dare un ordine a tutto ciò che può avvenire durante le interazioni e di cui dobbiamo tenere conto nella ricostruzione teorica dell’evento. In un secondo tempo, la successione di grafici viene tradotta in una successione di integrali numerici, ovvero, in poche parole, una formula, in cui non manchi nulla di rilevante. Tali grafici sono costituiti da linee che ricordano delle traiettorie percorse dalle particelle e assomigliano quindi ad un tentativo di descrizione degli eventi fisici. Tuttavia il concetto stesso di traiettoria è ambiguo quando utilizzato a livello microscopico: è questa la grande rivoluzione apportata dal principio di indeterminazione di Heisenberg alla fisica classica. Coerentemente a ciò, l’obiettivo di Feynman è infatti molto più diretto al calcolo di una grandezza che alla visualizzazione di un meccanismo microscopico: i diagrammi non sono un tentativo di descrivere cosa realmente avvenga alle particelle, ma solo di ottenere dei numeri che corrispondano, in ultima analisi, a quantità osservabili in laboratorio.

Questa constatazione mette in luce il carattere spiccatamente strumentalistico assunto dalla ricerca in fisica nell’ultimo secolo: in seguito al ridimensionamento delle possibilità esplicative di concetti classici come posizione, velocità, particella, onda, causa ed effetto, indotto dalla rivoluzione quantistica, la fisica ha dovuto rinunciare alla visualizzabilità delle sue idee e limitare le sue teorie ad un mondo di formule che sfuggono ai tentativi di comprensione in termini “meccanici” ma che sono in grado di costituire comunque un quadro coerente da cui è possibile ottenere valide predizioni di quantità osservabili.

Scendendo su di un livello più propriamente sociologico, la storia del nome del diagramma a pinguino può dare lo spunto per un’ulteriore istruttiva considerazione, che forse sorprenderà chi non conosca l’ambiente della ricerca. Un fisico, siamo negli anni ’70, che sta lavorando alla teoria di un certo tipo di quarks, un giorno perde una partita a freccette con i colleghi e si trova a dover pagare un pegno consistente nel dover assolutamente includere la parola “pinguino” nella sua successiva pubblicazione scientifica. Questo tipo di sfide ha un origine evidentemente goliardica, eppure non si esaurisce in ciò, anzi. Una sfida, anche scherzosa, è capace di fare percorrere nuove e inaspettate strade all’immaginazione. Questo episodio testimonia quindi la creatività diffusa che caratterizza l’ambiente scientifico, e i risultati a cui essa può condurre, a fronte magari di un immaginario collettivo che vede lo scienziato come una persona fredda e calcolatrice.

Anche la storia successiva ha per protagonista Feynman, ma non è per questa coincidenza che qui la associo alla precedente, ma per il problema epistemologico a cui essa indirizza.

Feynman racconta che la sua mentalità scientifica è maturata lentamente in lui anche grazie a suo padre che, quando lui era piccolo, gli narrava molte storie, arricchendole di considerazioni che aiutavano a visualizzare il racconto (3). Come esempio, Feynman riferisce che il padre, raccontandogli di un certo tipo di dinosauro, non si limitò a dirgli che esso aveva posseduto una testa larga un metro e un collo lungo tre metri, ma tradusse questa informazione in un’immagine: se quel dinosauro fosse stato lì, sarebbe riuscito a guardare attraverso la finestra della sua cameretta, ma non ad infilarci la testa. Questo per Feynman è il corretto approccio scientifico: mettere in relazione le misure, crearsi un’immagine nello spazio e nel tempo della successione degli eventi.

Nello stesso scienziato, Feynman, vediamo dunque entrambi gli approcci filosofici in contesa, il realismo e lo strumentalismo, riassumendo così quella contraddizione che resta irrisolta nella mentalità dei fisici contemporanei, molti dei quali non ne sono neppure consapevoli. Da una parte c’è il Feynman strumentalista, quello che si inventa dei grafici che sono solo segni utili per poter arrivare a dei numeri su cui ricercare l’accordo con i dati sperimentali, dall’altra c’è il Feynman realista, secondo il quale è vitale che la fisica proponga teorie in cui non si rinunci alla rappresentabilità nello spazio e nel tempo delle grandezze in gioco. Vale la pena di ricordare che Einstein combatté con convinzione negli ultimi decenni della sua vita il primo atteggiamento e propugnò il secondo.

Il terzo aneddoto riguarda una delle maggiori scoperte sperimentali del Novecento: la radiazione cosmica di fondo. Essa avvenne nel 1964 ad opera di A. Penzias e R. Wilson. I due, ricercatori dei Bell Laboratories, si stavano occupando di una serie di misure di interesse per lo più applicativo di una nuova grande antenna piazzata nel verde del New Jersey. Per settimane si trovarono impegnati a calibrare l’oggetto, che si ostinava a rivelare un segnale di fondo (“rumore”) che sporcava il segnale che era invece di loro interesse. Eliminarono quindi scrupolosamente uno ad uno i possibili problemi, addirittura si diedero da fare per scacciare dei piccioni che avevano fatto il nido nell’antenna, che ripassarono per bene ripulendola a fondo da tutto il guano depositato dai due volatili. A quel punto dovettero arrendersi: il rumore permaneva, sempre e comunque, e non era un errore di calibrazione. In pochi giorni i due ebbero l’occasione di parlarne con un amico fisico teorico, che si stava occupando proprio di calcolare, assieme ad altri, la radiazione di fondo implicata dalla nuova teoria del Big Bang. Cosi’ Penzias e Wilson furono gli unici ricercatori che, come disse qualcuno, cercarono guano e trovarono oro, mentre di solito, ai ricercatori, succede l’esatto contrario. Questo commento moraleggiante può essere utilizzato anche come compendio autoreferenziale delle conclusioni a cui si perviene osservando gli studi che hanno cercato di definire il corretto modo di produrre scienza. A quanto pare la scoperta del secolo di Penzias e Wilson non è frutto di una collezione scrupolosa ed imparziale di dati (Bacone), né di una serie di esperimenti volti a verificare la correttezza di un’ipotesi enunciata sulla base di una sequenza di proposizioni atomiche direttamente interpretabili secondo protocolli di laboratorio (Circolo di Vienna), né di una congettura sottoposta ad una serie di corroborazioni e confutazioni (Popper), né di un cambiamento irrazionale di prospettive, vocabolario e intenzioni (Kuhn). Forse gli si potrebbe adattare il solo anything goes di Feyerabend, il che è per l’appunto la ricetta di una non ricetta. Ovviamente la questione non è così semplice: prima e dopo la rivelazione del fondo a 3K, come venne battezzato facendo riferimento alla temperatura del corpo nero che produce uno spettro analogo, si sono susseguite varie congetture sulle caratteristiche che sarebbero dovute appartenere a tale radiazione, ed effettivamente si è sviluppato negli anni un continuo lavorìo di confronto-scontro-modifica dei calcoli con la teoria, fino ad assumere negli anni recenti i caratteri di quello che potremmo in effetti definire il paradigma attuale della cosmologia. Resta il fatto che quella prima rivelazione del fondo di radiazione nasce all’insegna di una coincidenza, di una serendipity, di una condizione fortuita in cui si trovarono gli uomini giusti, con le conoscenze giuste, nel posto giusto e al momento giusto. E con tutta l’umiltà necessaria per chinarsi a grattare via il guano dalla loro antenna.

Il quarto aneddoto è una vera e propria barzelletta e non sono in grado di risalire alla sua origine; posso solo dire che è più o meno diffusa tra i fisici, dove si tramanda di generazione in generazione. Dunque: c’è un esercito che progetta di cingere d’assedio una città fortificata; il re manda avanti una spia a raccogliere informazioni. Al rientro, la spia fa rapporto. “A quanto ammontano le forze del nemico?”. “Mille e quattro, sire”. “Mille e quattro? Perbacco, che accuratezza!” fa il re, orgoglioso dell’abilità dei suoi servizi segreti. “Ma come hai fatto?” “Semplice: ai quattro vertici della fortificazione ci sono quattro torri, e su ciascuna torre una guardia di vedetta; e questo fa quattro. E poi… va bé, dentro ci sarà un migliaio di persone!”. Il senso, non ci sarebbe bisogno di dirlo, è quello naturalmente del saper utilizzare i numeri che si riferiscono ad enti concreti con la consapevolezza che essi derivano da un processo di misura, il quale porta sempre con sé una certa incertezza, la “barra d’errore”. Se diciamo, in seguito ad una stima ad occhio, che i cittadini sono un migliaio, intendiamo dire probabilmente che il loro numero si aggira tra gli ottocento e i milleduecento, e quindi non ha senso specificare quelle quattro unità stabilite con tanta precisione. È lo stesso motivo per cui le persone si danno appuntamento per pranzo alle 12.30 o alle 12.40, e mai alle 12.32. Il discorso ci appare molto ragionevole ma, se lo estendiamo appena un po’, anche nella vita reale fuori dai laboratori, troviamo situazioni dove in effetti il concetto di “barra d’errore” è tutt’altro che utilizzato. Occorre poi sottolineare che quanto più è ambigua la possibilità di utilizzare i numeri per valutare una situazione, tanto più bisognerebbe tenere a mente questa idea di una banda di oscillazione. Invece, sovente, succede proprio il contrario.

Voglio associare questo ad una situazione reale e scolastica, anche di stretta attualità. Qualche volta mi sono trovato a discutere di voti e di arrotondamenti di voti con altri colleghi, ad esempio in occasione delle famigerate griglie di valutazione che vanno predisposte in occasione dell’esame di stato. Ho visto discussioni su decimi, o addirittura centesimi di voto, senza realizzare che la barra di errore che associamo implicitamente alla nostra valutazione è di ordini di grandezza superiore.

A volte questa volontà di “numerizzazione” spinta, che viene equivocata per scienza, entra là dove non dovrebbe neppure entrare, risultando controproducente e dimostrando una consapevolezza distorta dell’utilizzo della quantificazione. Personalmente credo, ad esempio, che, appiattendo la valutazione dell’educazione scolastica sulle prove INVALSI o PISA, si rischi una banalizzazione degli obiettivi della scuola da una parte, e un oltraggio ai buoni servizi prestati altrimenti dalla matematica all’umanità, dall’altra parte.

L’altra caratteristica eminente della fisica, assieme al legame stabilito tra il mondo dei numeri e quello delle misure, è quello della controllabilità, ovvero del confronto della teoria con la realtà, che avviene proprio grazie alla traduzione dei modelli in operazioni di misura. Ci sono due figure retoriche, una molto nota, quella del tacchino induttivista, attribuita da Popper a Russell, ma resa famosa dallo stesso Popper, e una destinata, forse, a diventarlo, quella del drago nel garage di Carl Segan. Il lettore interessato può trovarne una descrizione resa in prospettiva didattica in (2).

Infine, vorrei concludere questo percorso con la risposta che Michael Faraday (1791-1867) diede ad un primo ministro in visita presso il suo laboratorio. Richiesto dell’importanza che avrebbe mai potuto avere una sua scoperta (pare relativa all’elettrochimica, e non all’induzione elettromagnetica da cui deriveranno i motori elettrici), il fisico rispose Why sir, there is the probability that you will soon be able to tax it(4). Induce, se non una riflessione di carattere epistemologico, una riflessione di carattere sociologico e sempre di attualità, tanto più problematica quanto più ci si trovi in tempi di crisi economica. Non si può dare facilmente torto a Faraday, infatti: la ricerca scientifica, anche quella più teorica e senza alcun orizzonte pratico in vista, ha dimostrato, col tempo, di saper indurre fondamentali ricadute tecniche e tecnologiche, capaci di modificare non solo la vita pratica, ma anche la struttura sociale della civiltà. Con una battuta e senza circonlocuzioni Faraday ha messo in luce gli effetti concreti legati alla pratica della scienza, anche se, come per tanti scienziati, il suo amore per la scienza fu dettato esclusivamente dall’amore per la conoscenza e per la verità. Quella stessa verità che, come un lampo, può balenare talvolta nelle nostre menti tramite l’insostituibile sintesi di una battuta.

Bibliografia

(1) R. A. Berk, Student ratings of 10 strategies for using humor in college teaching, Journal on Excellence in College Teaching, 7, 71 (1996)

(2) L. Colletti, On dragons and turkeys: physics for future citizens, School Science Review, June 2010, 91, 337 (2010)

(3) R. P. Feynman, Che t’importa di ciò che dice la gente (ed. orig. 1988)

(4) I. B. Cohen, Faraday and Franklin’s “Newborn Baby”, Proceedings of the American Philosophical Society, vol. 131, no. 2 (1987)

Richard Feynman in un famoso ritratto (fonte: APS Photo Archive)